TV / PROGRESIÓN GEOMÉTRICA SEMANA 6 (DÍA 4)

Reto 1:

Encontrar la progresión geométrica que permita cubrir con fichas un tablero con 242 casillas, siguiendo las reglas del juego encasillado.

Utilizaremos la suma de n términos:

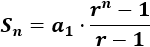    = 242      242 = 2 x 121             Datos:

Sn= 2 (r(n)-1) 242                                                                a1 = 2

             r -1                                        3(5) = 243                  n = 5

Sn= r(n)-1= 121                                                                    r = 3

          r-1

3 - 1 = 121 → 3(n) - 1 = 121 →  3(n)-1 = 242 → 3(n) = 243

3 - 1                    2

La progresión Geométrica seria:

2       ;        6        ;        18       ;      54      ;        162

                                              x3               x3                x3             x3

Ahora aplicamos la propiedades de la progresión geométrica:
Multiplicamos los términos extremos:          Multiplicamos los términos equidistantes:
                  2 x 162 = 324                                                            6 x 54 = 324

Reto 2:

Averiguar como se podría utilizar las formulas y las propiedades de la progresión

geométrica para resultar ganador en el juego "encasillados". Explica tus respuestas

Explicación:

Como vemos la progresión geométrica nos ayuda a ganar el juego de encasillados, calculando la suma de los n términos nos ayuda a saber como cubrir el tablero con 242 casillas que hay sin sobrar casillas o faltar casillas y en el caso de la propiedad de la progresión geométrica ayuda confirmar si la progresión esta bien o no, ya que el producto de dos términos equidistantes es igual al producto de los extremos.