Reto 1:
Identificar una situación real donde puedan hacer uso de las distintas fórmulas qué están en sus cuadernos de trabajo
Situación Real:
Una microempresa viendo que la tasa de infectados esta incrementando decide emprender en la confección de mascarillas para que las personas no se contagien del COVID-19. La empresa dispone de 1 semana para la elaboración de mascarillas. Sabiendo que el primer día confeccionan 100 mascarillas y en el segundo día el doble del anterior.
¿En el día 7 cuantas mascarillas hay?¿Cuantas mascarillas habrá del día 1 hasta el día 7?
Datos: Reemplazamos utilizando la formula general:
a1 = 100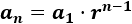 
an = 100*2(7-1) → an = 100*2(6) → an = 100*64
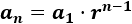an = 100*2(7-1) → an = 100*2(6) → an = 100*64
r = 2
an = ? → 6 400
Ahora utilizamos la suma de los n términos para saber la cantidad de mascarillas se han confeccionado:
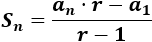
Reemplazamos valores:
Sn = 6 400 * 2 - 100 = 12 800 - 100
2 - 1 1
Sn = 12 700
Respuesta: En el día 7 hay 6 400 mascarillas, durante toda la semana de fabricación hubo
12 700 mascarillas.
La progresión geométrica es creciente por que el primer termino es positivo, y si la razón es mayor que 1.
Ahora utilizamos la suma de los n términos para saber la cantidad de mascarillas se han confeccionado:
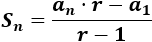
Reemplazamos valores:
Sn = 6 400 * 2 - 100 = 12 800 - 100
2 - 1 1
Sn = 12 700
Respuesta: En el día 7 hay 6 400 mascarillas, durante toda la semana de fabricación hubo
12 700 mascarillas.
La progresión geométrica es creciente por que el primer termino es positivo, y si la razón es mayor que 1.
No hay comentarios.:
Publicar un comentario